 | |  |
| |
Математика в помощь ARIS-аналитику.
C помощью теории графов мы решим три популярных задачи скриптов в ARIS: проверка целостности моделей, определение последовательности выполнения процессов, определение максимального срока выполнения процесса.
Определение графа.
Модель eEPC описывает деятельность в виде последовательности выполнения отдельных ее элементов. Модель представляет собой граф, состоящий из вершин – объектов модели, а также дуг – связей между ними.
Множество вершин графа примем
X = {S1, …, Sn1, F1, …, Fn2, D1, …, Dn3, I1, …, In4, P1, …, Pn5, R1, …, Rn6} (1),
где Si – события в рамках одной модели, Fi – функции, Di – документы (информационные носители), Ii – исполнители функций, Pi – информационные системы, Ri – правила ветвления/слияния процесса.
Множество дуг графа примем:
V = {d1, …, dn7} (2),
где di – дуги графа в рамках одной модели:
di = di(Sj, Fk) = -di(Fk, Sj) – направленные дуги между событиями и функциями;
di = di(Sj, Rk) = -di(Rk, Sj) – направленные дуги между событиями и правилами ветвления/слияния процесса;
di = di(Rj, Fk) = -di(Fk, Rj) – направленные дуги между правилами ветвления/слияния процесса и функциями;
di = di(Rj, Rk) = -di(Rk, Rj) – направленные дуги между двумя разными правилами ветвления/слияния процесса;
di = di(Dj, Fk) = -di(Fk, Dj) – направленные дуги между документами и функциями;
di = di(Ij, Fk) = di(Fk, Ij) – ненаправленные дуги между исполнителями и функциями;
di = di(Pj, Fk) = di(Fk, Pj) – ненаправленные дуги между информационными системами и функциями.
В общем случае данный граф обладает следующими свойствами:
• является связным;
• является смешанным, т.к. содержит направленные и ненаправленные дуги;
• не является деревом;
• не имеет циклы;
• не имеет петель;
• не является эйлеровым.
Проверка целостности моделей.
Проверка целостности моделей производится при работе многих скриптов и служит гарантом корректности результатов их работы.
Для этого рассматриваются граф (1) со всеми его элементами. Известно, что если любые две вершины графа можно соединить цепью, то граф является связным. Для проверки связности достаточно выбрать одну вершину графа и проверить, соединена ли она цепью со всеми остальными вершинами.
Выберем вершину S1 (инициирующее событие в процессе) методом перебора вершин и поиска той, в которую не входит ни одна из направленных связей. Производится поиск всех смежных вершин X(S1) = X1, … Xn. Найденные вершины помечаются как пройденные, чтобы более не обращаться к ним в процессе поиска цепи. Далее действие повторяется итерационно для каждой смежной Xi до тех пор, пока не останется еще не помеченных вершин.
Если как минимум одна вершина графа не окажется помеченной как пройденная, то граф не является связным, а модель целостной.
Определение последовательности выполнения процессов.
Определять последовательность функций в процессе приходится в большинстве скриптов, которые формируют какой-либо отчет по модели. Связано это, прежде всего, с необходимостью идентификации элементов модели и структуризации отчета.
Для определения последовательности выполнения процесса из всех элементов модели используются лишь те, которые имеют ориентированные исходящие или входящие дуги за исключением входов и выходов функций.
Граф (1) для решения данной задачи преобразуется в:
X = {S1, …, Sn1, F1, …, Fn2, R1, …, Rn6} (3),
где все элементы являются равнозначными друг другу.
Поиск вершин в ширину или глубину относительно корня графа S1 не дает необходимой последовательности выполнения процесса (см. рисунок 1).
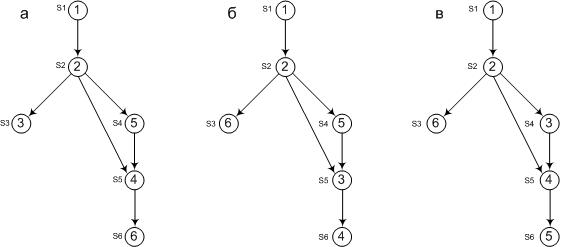
Рисунок 1. Порядок обхода вершин графа: а) в ширину, б) в глубину, в) искомый порядок.
Как видно из рисунка, метод обхода графа в ширину не подходит, а метод обхода в глубину четко разграничивает ветки процесса, однако не корректно соблюдает логику последовательности в подграфе, не являющемся деревом. В примере X2 = {S2, S4, S5, S6}.
Для решения этой задачи произведем с результатом следующие действия:
1. Найдем между всеми парами вершин графа путь, состоящий из направленных дуг.
К примеру, путь между вершинами S1 и S4 состоит ид двух дуг d = d1(S1, S2) + d2(S2, S4).
2. Найдем путь между этими же парами вершин, но в обратном направлении.
К примеру, путь между вершинами S4 и S1 состоит ид двух дуг d = - d2(S1, S2) - d1(S2, S4).
3. В случае если между парой вершин существует отрицательный путь и не существует положительного пути, это означает, что между ними есть явная последовательность. Порядковые номера таких вершин необходимо поменять местами.
К примеру, путь между вершинами S4 и S5 имеет положительный знак, а между S5 и S4 - отрицательный. После смены их номеров ситуация повторяется для пары вершин S5 и S6 (см. рисунок 2).
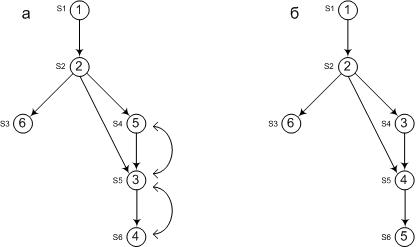
Рисунок 2. Порядок корректировки графа после обхода вершин в глубину.
Таким образом определяется порядок выполнения процесса, который используется в большинстве скриптов для идентификации функций и формирования ссылок на них.
Определение максимального срока выполнения процесса.
Часто возникает необходимость при формировании с помощью скрипта аналитической информации о длительности процесса, определять максимальный срок исполнения процесса. К примеру, он не может быть больше, чем утвержденный соответствующим нормативным документом.
Для решения этой задачи необходимо решить аналогичную задачу в терминах теории графов: поиск длиннейшего пути. Каждая дуга имеет вес Ni = N( di(Si,Si+1) ), фактически являющийся длительностью выполнения функции, из которой выходит дуга.
Из теории графов известно, что чтобы задачу о максимальном (длиннейшем) пути – достаточно изменить знаки дуг на противоположные и решить задачу о кратчайшем пути. Для существования решения задачи о максимальном пути необходимо и достаточно отсутствия контуров положительной длины.
Применим к графу (3) алгоритм поиска пути Флойда с отрицательными значениями дуг.
Пусть все вершины орграфа последовательно пронумерованы от 1 до n. Алгоритм Флойда использует матрицу A(1…n, 1…n), в которой находятся длины кратчайших путей:
Aij=Nij, если i≠j;
Aij=0, если i=j;
Aij=∽, если отсутствует дуга, соединяющая вершины Si и Sj.
Над матрицей A выполняется n итераций. После k-той операции Aij содержит значение наибольшей длины пути из вершины i в вершину j, причем путь не проходит через вершины с номерами больше k. Вычисление на k-ой итерации выполняется по формуле:
Aij(k) = min(A(k-1)ij, A(k-1)ik + A(k-1)kj).
Приведем пример вычисления для графа (см рисунок 3):
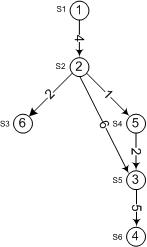
Рисунок 3. Определение наибольшего пути графа.
Начальные условия и конечный результат соответствуют матрицам:
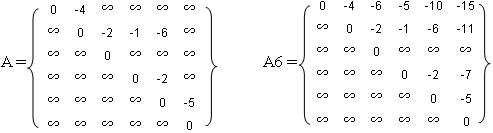
A(1,6) = -15, это означает, что максимальный путь лежит между вершинами от S1 к S6 и составляет 15 единиц.
Таким образом, с помощью теории графов мы решили три популярных задачи скриптов в ARIS: проверка целостности моделей, определение последовательности выполнения процессов, определение максимального срока выполнения процесса.
Литература
1. В.Н. Бурков, Д.А. Новиков. Элементы теории графов.
|
Категория: Программисту ARIS Script | Добавил: easyaris (17.02.2008)
| Автор: Селезнев Константин 
|
| Просмотров: 3518
|
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] | |
 | |  |
|
|





